The Scenario: SolVault's Collateral Risk Pricing
Imagine you're building SolVault, a decentralized lending protocol on Solana. Your protocol needs to calculate liquidation penalties that scale with the risk of different collateral types. Riskier assets require higher penalties to protect the protocol.
Here's how it works:
- Users deposit various tokens as collateral to borrow against
- Each collateral type has a risk score based on volatility and liquidity
- Liquidation penalties increase exponentially with risk to discourage risky positions
- The penalty formula ensures protocol solvency during market stress
The challenge comes in calculating the liquidation penalty using a risk-based model:
liquidation_penalty = min_penalty × risk_multiplier^(volatility_score)This exponential relationship creates appropriate incentives. For example:
- Low-risk assets (stablecoins): minimal penalty
- Medium-risk assets (SOL, ETH): moderate penalty
- High-risk assets (small caps): significant penalty
- The exponential curve ensures penalties scale appropriately with risk
When risk_multiplier is 1.5 and volatility_score is 3.0, the penalty multiplier would be 1.5^3.0 = 3.375×, making the penalty 3.375 times the minimum.
The Floating-Point Dilemma
The natural implementation would use Rust's powf function:
pub fn calculate_liquidation_penalty_v1(
asset_config: &AssetConfig,
market_conditions: &MarketConditions,
) -> f64 {
let base_penalty = asset_config.min_penalty_percent;
let risk_factor = asset_config.risk_multiplier;
let volatility = market_conditions.calculate_volatility_score();
// Exponential scaling based on current volatility
let penalty_multiplier = risk_factor.powf(volatility);
let final_penalty = base_penalty * penalty_multiplier;
// Cap at maximum allowed penalty
final_penalty.min(asset_config.max_penalty_percent)
}While this works perfectly in tests, it has a subtle issue: the powf function may return slightly different results on different hardware architectures. The Rust documentation notes that the precision can vary by approximately 10-16, which might seem negligible but if implemented in the same way in the SVM, they could violate Solana's requirement for deterministic execution.
Determinism: The Unbreakable Covenant of Blockchain
To grasp why floating-point math is so hazardous on-chain, one must first understand the non-negotiable principle of determinism. In computer science, a deterministic algorithm is one that, given a particular input, will always produce the same output while passing through the same sequence of states. In the context of a blockchain, this principle is elevated to an unbreakable covenant. It dictates that every validator in a decentralized network, when processing the same transaction, must arrive at the exact same resulting state.
A powerful mental model for a blockchain is that of a distributed, deterministic state machine. The current state of the entire ledger, all account balances, all stored data, is one massive, agreed-upon state. A transaction is an input that causes the machine to transition to a new state. For the network to maintain consensus, every node must independently compute this state transition and arrive at an identical result. If one node calculates a new account balance of 100 and another calculates 101, the consensus is broken. The chain cannot proceed, as there is no single source of truth.
Why Floating-Point Numbers Break the Covenant
Floating-point numbers are the antithesis of determinism. The IEEE 754 standard for floating-point arithmetic, while ubiquitous, does not guarantee bit-for-bit identical results across different hardware architectures or even different versions of the same compiler or software library. Minor variations in how a CPU's floating-point unit (FPU) is implemented or how the LLVM compiler (used by Solana) handles an operation can lead to minuscule differences in precision and rounding.
A calculation that produces 1.000000001 on one validator's Intel CPU and 1.000000002 on another's AMD CPU represents a consensus failure. While this discrepancy seems small, in a system built on cryptographic certainty, there is no such thing as "close enough." The output must be identical. Thankfully, on Solana all floating-point operations are emulated in the same way on all the nodes, therefore, this risk of breaking consensus is eliminated. However, due to this emulation there's a significant performance penalty.
Solana's Official Stance and the Performance Penalty
The Solana documentation warns against the use of floating-point numbers, noting that on-chain programs support only a limited subset of Rust's float operations. Any attempt to use an unsupported operation will result in an "unresolved symbol error" at deployment.
More importantly, even the supported float operations come with a significant performance penalty. Because they are not handled natively and must be emulated in software via LLVM's float built-ins, they consume far more compute units (CUs) than their integer-based counterparts.
Developers are in a constant battle against the per-transaction compute budget of 200,000 CUs, and choosing inefficient operations can limit a program's capabilities.
The performance difference is not trivial. As shown in Table 1, based on Solana Program Library math tests, basic floating-point operations can be over 20 times more expensive than their u64 equivalents.
Table 1: Compute Unit Cost: Integer vs. Floating-Point Operations on Solana
This table show that using floats is grossly inefficient, consuming a disproportionate share of a transaction's limited compute budget.
The DeFi Dilemma: A Case Study in Liquidation Risk
Back to our SolVault
liquidation_penalty = min_penalty × risk_multiplier.powf(volatility_score)In this formula:
- min_penalty is the base liquidation penalty (e.g., 5%)
- risk_multiplier is a value like 1.5, representing how much riskier this asset is compared to the baseline
- volatility_score is a dynamic value between 1 and 5 based on current market conditions
- The result determines how much of a borrower's collateral is seized as a penalty during liquidation
This calculation, using powf, will be executed independently by every Solana validator that processes a liquidation transaction.
The Invariant Check: The Protocol's Safety Net
Robust lending protocols are built upon a foundation of mathematical assertions known as "invariants." These are checks that must hold true at the end of every transaction to ensure the protocol's solvency and logical consistency. A critical invariant for liquidations is:
total_collateral_value >= total_debt_value * min_collateral_ratioThis ensures the protocol maintains adequate over-collateralization. Additionally, liquidation transactions must satisfy:
penalty_collected + debt_repaid <= collateral_seized_value
If these checks fail, the program is designed to panic and revert the transaction. This is a safety mechanism to prevent the protocol from becoming under-collateralized or allowing unfair liquidations.
The Trigger: Death by a Single Lamport
Here is where the non-determinism of powf creates a disaster. Consider a volatile asset with:
- risk_multiplier = 1.8
- volatility_score = 3.2
When different validators compute 1.8^3.2, some might arrive at 4.7829672…8 while others, due to subtle differences in their floating-point hardware or software stack, calculate 4.7829672…9. Note that one value ends with an 8 and the other one with a 9.
Now imagine a critical liquidation scenario:
- A position with 1,000,000 lamports of collateral needs liquidation
- The debt to repay is 700,000 lamports
- One validator calculates penalty = 47,829 lamports
- Another validator calculates penalty = 47,830 lamports (1 lamport higher)
When the liquidator attempts to seize exactly 747,829 lamports (debt + penalty), the transaction succeeds on some validators but fails on others where the penalty was calculated as 47,830. The invariant check penalty_collected + debt_repaid <= collateral_seized_value fails by a single lamport.
The Cascade Effect
The consequence is immediate and severe: the program panics, and the liquidation is reverted. But this isn't just about one failed transaction:
- Liquidation Gridlock: If the position cannot be liquidated due to non-deterministic calculations, it remains in the system, potentially becoming further underwater as market conditions worsen.
- Protocol Insolvency: Unable to liquidate risky positions, the protocol accumulates bad debt.
- Oracle Exploitation: Sophisticated attackers could potentially exploit the non-determinism by crafting positions that are "unliquidatable" on certain validators, manipulating the system while protected from liquidation.
- Contagion Risk: Other protocols that rely on SolVault for lending or that accept its receipt tokens as collateral begin operating with flawed assumptions about the protocol's solvency.
The Safe Harbor: Deterministic Approximation with Taylor Series
Given the clear dangers of powf, developers need a secure and deterministic alternative for calculating fractional powers. While the standard for most on-chain math is to use fixed-point libraries like spl-math, their built-in power functions, such as checked_pow, typically require an integer exponent, leaving a tooling gap for fractional exponents.
The solution lies not in finding a perfect replica of powf, but in using a deterministic approximation. A particularly effective method for this is the Taylor series expansion.
Approximating with Polynomials
The core idea of a Taylor series is to approximate a complex, non-linear function, in this case, xy, with a simple, deterministic polynomial. A polynomial is just a sum of terms with integer powers, which can be computed using only the fundamental arithmetic operations of addition, subtraction, and multiplication. These are operations that can be performed deterministically and efficiently on-chain using fixed-point math.
For the function f(x)=xy, the Taylor series expanded around x=1 provides an excellent approximation, especially when x is close to 1, which is common in DeFi for representing small growth factors (e.g., 1.001).
Visualizing the Solution's Safety
The analysis of this approximation method reveals its suitability for the on-chain environment. The following plots, which model the function xy, illustrate the behavior of the Taylor series approximation against the exact mathematical function for a domain relevant to DeFi: a base x (growth factor) in the range [1, 1.1] and an exponent y (time/fee factor) in the range .

Figure 1: Comparison of the Taylor approximation (red) versus the exact power function (blue) for a fixed exponent (left) and a fixed base (right). Note the consistent "Underestimation gap".
As seen in Figure 1, the Taylor approximation (orange line) closely tracks the exact value (blue line). More importantly, it consistently stays just below the exact value. This "underestimation gap" is not a flaw; it is the approximation's most critical security feature.
The error heatmap provides a comprehensive view of this behavior across the entire domain of interest.
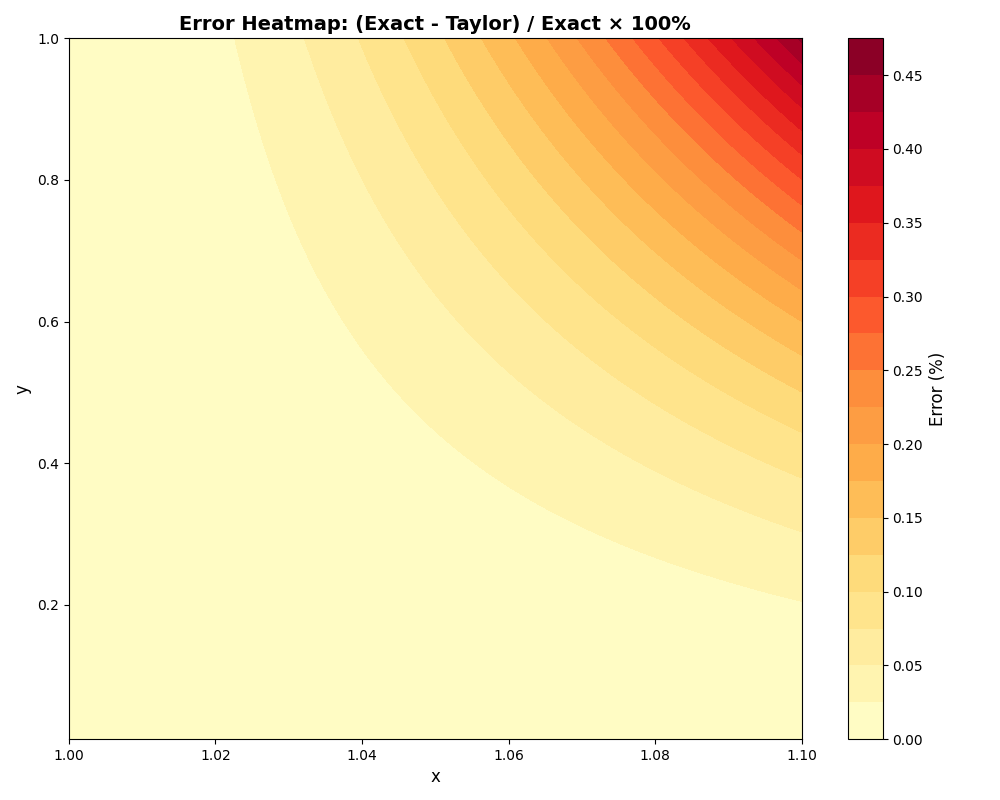
Figure 2: A heatmap visualizing the relative error of the Taylor approximation.
The heatmap in Figure 2 visualizes the percentage error of the approximation. The fact that the entire map is shaded in red (representing negative error) offers visual proof that the approximation always underestimates the true value. The error is also bounded and predictable, with a maximum error of approximately 0.45% and a mean error of just 0.05% within this domain.
This consistent underestimation represents a deliberate choice to "fail safe." In financial software, there are two primary types of errors: those that harm the protocol and those that harm the user.
- Over-crediting a user (e.g., giving them too much yield) harms the protocol by draining its treasury. This can lead to insolvency, a failure that affects all users.
- Under-crediting a user (e.g., giving them slightly less yield) is unfavorable for that individual user but protects the integrity and solvency of the system as a whole.
By guaranteeing that it will never over-credit a user's yield, the Taylor series approximation systematically prioritizes protocol solvency over perfect, user-level precision. This transforms the approximation from a mere mathematical tool into a robust risk management strategy tailored for the adversarial on-chain environment. It encourages a paradigm shift for developers: instead of seeking perfect replication of off-chain math, the goal should be to design provably safe approximations that fit within the specific risk profile and acceptable error bounds of the protocol.
Conclusion
The allure of a simple, one-line solution for a complex mathematical problem is powerful. Yet, on the blockchain, this simplicity can be deceptive and dangerous. Floating-point numbers and the functions that rely on them, like powf, are unsafe and incur significant performance penalties. Solana developers must be deliberate and deeply skeptical in their choice of mathematical tools. The default approach must always be integer-based fixed-point math. For more complex functions like fractional exponentiation, the path forward is not to seek perfect replication of off-chain behavior but to design and implement provably safe approximations, such as the Taylor series. This method provides a result that is not only deterministic and efficient but is also engineered with a "fail-safe" property that prioritizes the solvency and security of the protocol.
Ultimately, building robust systems is synonymous with building predictable ones. The constraints of the SVM are not limitations to be circumvented; they are the very features that enable the trust, security, and reliability of the decentralized applications that hold real value. At Adevar Labs, we treat math as a security boundary. If you're relying on nuanced approximations, fixed-point arithmetic, or custom invariants, it's worth having that logic reviewed.
Ship Safely!
References
- Deterministic algorithm - Wikipedia, accessed July 2, 2025
- What Does Determinism Mean in Blockchain? - Nervos Network, accessed July 2, 2025
- Limitations | Solana, accessed July 2, 2025
- Arithmetic and Basic Types in Solana and Rust - RareSkills, accessed July 2, 2025
- Solana Arithmetic: Best Practices for Building Financial Apps - Helius, accessed July 2, 2025

 Button Text
Button Text





